20. Getting integral and fractional parts from a double
You know, there are some problems which are very easy if you know the solution and seem very difficult if you don’t? This is exactly this kind of problem. The solution is quite simple as you can see in the following code:
double value = -9.33543545;
double fractionalPart = value % 1;
double integralPart = value – fractionalPart;
This was easy; I don’t think you need further explanations. But this approach is not quite accurate. I mean the integral part is -9, but this returns -9.0. And, the fractional part is -0.33543545, but the returned value is -0.3354354500000003.If we need a more accurate result then using BigDecimal is more useful:
BigDecimal bd = BigDecimal.valueOf(value);
int integralPart = bd.intValue();
double fractionalPart = bd.subtract(
BigDecimal.valueOf(integralPart)).doubleValue();
This time, the results are -9 and -0.33543545.
21. Testing if a double number is an integer
First of all, let’s consider the following expected results (false means that the double is not an integer):
double v1 = 23.11; // false
double v2 = 23; // true
double v3 = 23.0; // true
double v4 = Double.NaN; // false
double v5 = Double.NEGATIVE_INFINITY; // false
double v6 = Double.POSITIVE_INFINITY; // false
Most probably, the first solution for testing if a double number is an integer consists of a simple cast as follows:
public static boolean isDoubleIntegerV1(double v) {
return v == (int) v;
}
But, there are several other options. For instance, we can rely on modulus as follows:
public static boolean isDoubleIntegerV2(double v) {
return v % 1 == 0;
}
Or, on the Math.floor() and Double.isFinite() methods. If the given double is a finite number and is equal to the result of Math.floor() then it is an integer:
public static boolean isDoubleIntegerV3(double v) {
return ((Math.floor(v) == v) && Double.isFinite(v));
}
We can also replace this equality via Math.ceil():
public static boolean isDoubleIntegerV4(double v) {
return (Math.floor(v) == Math.ceil(v)
&& Double.isFinite(v));
}
Moreover, we can combine Double.isFinite() with Math.rint() as follows:
public static boolean isDoubleIntegerV5(double v) {
return ((Math.rint(v) == v) && Double.isFinite(v));
}
Finally, we can rely on Guava’s DoubleMath.isMathematicalInteger():
public static boolean isDoubleIntegerV6(double v) {
return DoubleMath.isMathematicalInteger(v);
}
But, which of these approaches has a better performance? On which one you are betting? Well, let’s see what a benchmark has to say:
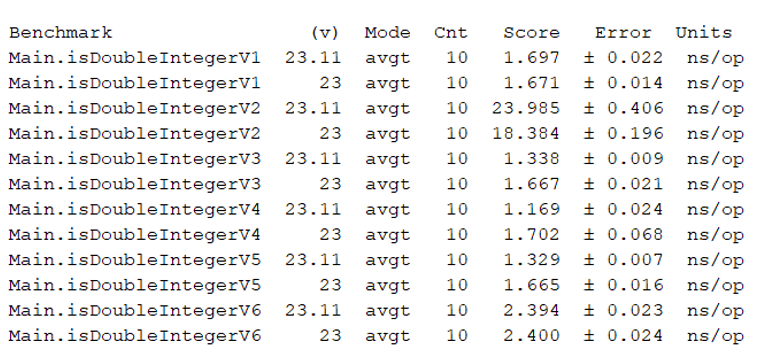
Figure 1.19 – Benchmark results
Based on these results, a conclusion is quite obvious the solution that relies on modulus should be avoided. And, the Guava solution seems to be slightly slower than the rest.