24. Collecting all prime factors of a given number
A prime number is a number divisible by itself and 1 (for instance, 2, 3, and 5 are prime numbers). Having a given number, we can extract its prime factors as in the following figure:
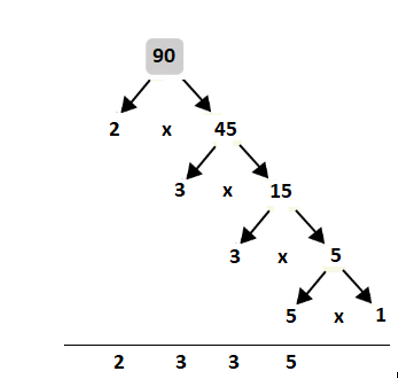
Figure 1.22 – Prime factors of 90 are 2, 3, 3, and 5
The prime factors of 90 are 2, 3, 3, and 5. Based on figure 1.22, we can elaborate an algorithm to solve this problem as follows:
Define a List for collecting prime factors of the given v Initialize a variable s with 2 (the smallest prime number) If v % s is 0, collect s as a prime factor and compute new v as v / s If v % s is not 0 then increase s by 1 Repeat step 3 as long as v is greater than 1 In code lines, this O(n) algorithm (O(log n) for composite numbers) can be expressed as follows:
public static List<Integer> factors(int v) {
List<Integer> factorsList = new ArrayList<>();
int s = 2;
while (v > 1) {
// each perfect division give us a prime factor
if (v % s == 0) {
factorsList.add(s);
v = v / s;
} else {
s++;
}
}
return factorsList;
}
In the bundled code, you can find two more approaches. Moreover, you’ll also find an application that counts the number of primes less than the given number, v (v should be positive).
25. Computing the square root of a number using the Babylonian method
Believe it or not, the ancient Babylonians (around 1500 BC) knew how to estimate square roots long before the popular method discovered by Newton.Mathematically speaking, the Babylonian approach for estimating the square root of v > 0 is the recurrence relation from the following figure:
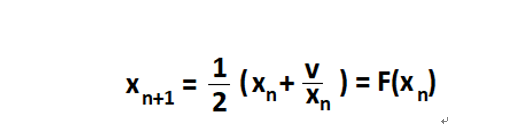
Figure 1.23 – The recurrence relation of Babylonian square root approximation
The recurrence formula starts with an initial guess of x0. Next, we calculate x1, x2, …, xn by substituting xn-1 in the formula on the right-hand side and evaluating the expression.For instance, let’s try to apply this formula for estimating the square root of 65 (the result is 8.06). Let’s start with x0 as 65/2, so x0=32.5, and let’s calculate x1 as:x1 = (x0 + v/x0)/2 → x1 = (32.5 + 65/32.5)/2 → x1 = 17.25Having x1, we can calculate x2 as follows:x2 = (x1 + v/x1)/2 → x2 = (17.25 + 65/17.25)/2 → x2 = 10.5Having x2, we can calculate x3 as follows:x3 = (x2 + v/x2)/2 → x3 = (10.5 + 65/10.5)/2 → x3 = 8.34We are getting closer to the final result. Having x3, we can calculate x4 as follows:x4 = (x3 + v/x3)/2 → x4 = (8.34 + 65/8.34)/2 → x4 = 8.06Done! After 4 iterations, we found that the square root of 65 is 8.06. Of course, being an approximation of the real value, we can continue until we reach the desired precision. More precision involves more iterations.The algorithm that is based on the Babylonian approach to approximate the square root of v > 0 has several steps as follows:
To start, choose an arbitrary positive value x (the closer to the final result the fewer iterations are needed). For instance, we start with x = v/2 as the initial guess.
Initialize y = 1 and choose the desired precision (for instance, e = 0.000000000001).
Until the precision (e) is achieved do the following:
- Calculate the next approximation (xnext) as the average of x and y
- Use the next approximation to set y as v/xnext
So, in code lines we have the following snippet:
public static double squareRootBabylonian(double v) {
double x = v / 2;
double y = 1;
double e = 0.000000000001; // precision
while (x – y > e) {
x = (x + y) / 2;
y = v / x;
}
return x;
}
In the bundled code, you can also see an implementation useful if you know that v is a perfect square (for instance, 25, 144, 169, and so on).